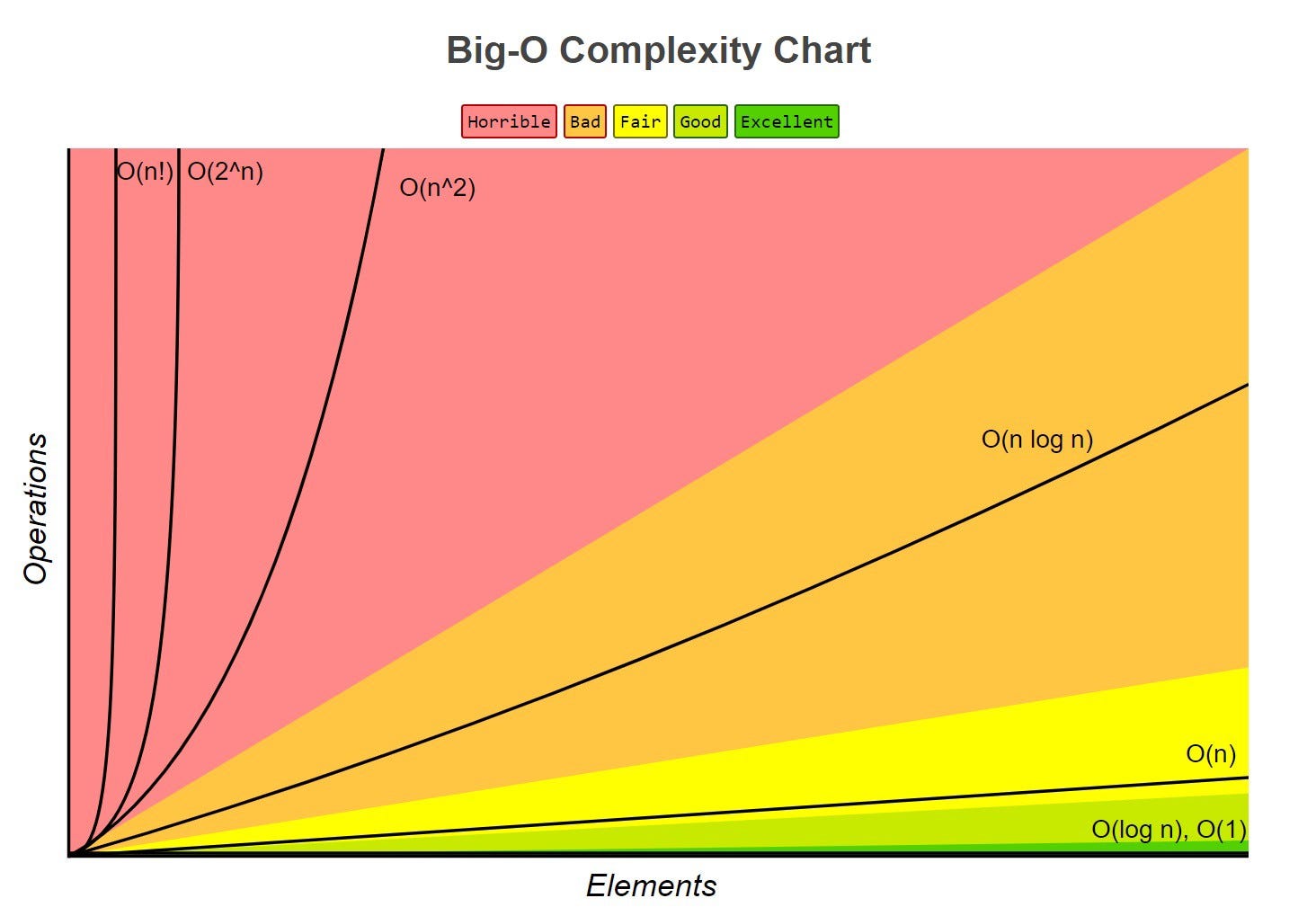
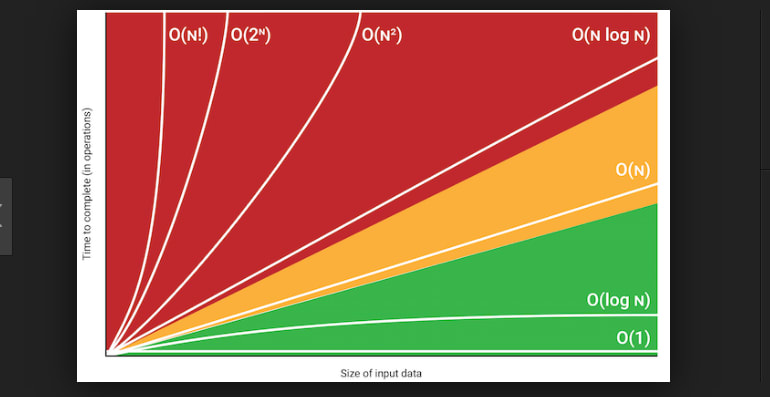
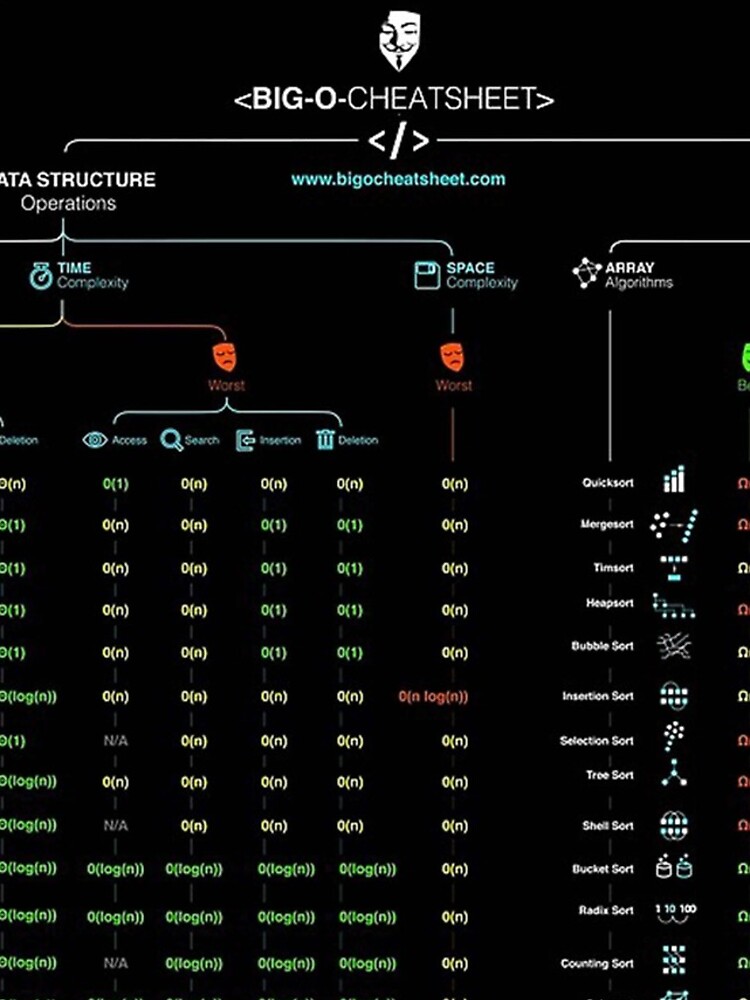
- Big O (O) describes the upper. Below is a cheat-sheet on the time and space complexity of typical algorithms. Big O Cheatsheet for Common Algorithms Solution to.
- Big-O Notation Cheat Sheet: quick answers to Big-O questions Oct 15, 2020 - 5 min read Big O notation (sometimes called Big omega) is one of the most fundamental tools for programmers to analyze the time and space complexity of an algorithm. Big O notation is an asymptotic notation to measure the upper bound performance of an algorithm.
No files in this folder. Sign in to add files to this folder.
Sorting algorithms are a fundamental part of computer science. Being able to sort through a large data set quickly and efficiently is a problem you will be likely to encounter on nearly a daily basis.
Here are the main sorting algorithms:
| Algorithm | Data Structure | Time Complexity - Best | Time Complexity - Average | Time Complexity - Worst | Worst Case Auxiliary Space Complexity |
|---|---|---|---|---|---|
| Quicksort | Array | O(n log(n)) | O(n log(n)) | O(n^2) | O(n) |
| Merge Sort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Select Sort | Array | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Bucket Sort | Array | O(n+k) | O(n+k) | O(n^2) | O(nk) |
| Radix Sort | Array | O(nk) | O(nk) | O(nk) | O(n+k) |
Another crucial skill to master in the field of computer science is how to search for an item in a collection of data quickly. Here are the most common searching algorithms, their corresponding data structures, and time complexities.
Time Complexity Cheat Sheet
Here are the main searching algorithms:
| Algorithm | Data Structure | Time Complexity - Average | Time Complexity - Worst | Space Complexity - Worst |
|---|---|---|---|---|
| Depth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Breadth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Binary Search | Sorted array of n elements | O(log(n)) | O(log(n)) | O(1) |
| Brute Force | Array | O(n) | O(n) | O(1) |
| Bellman-Ford | Graph of |V| vertices and |E| edges | O(|V||E|) | O(|V||E|) | O(|V|) |
Graphs are an integral part of computer science. Mastering them is necessary to become an accomplished software developer. Here is the data structure analysis of graphs:
Big O Cheat Sheet Pdf
| Node/Edge Management | Storage | Add Vertex | Add Edge | Remove Vertex | Remove Edge | Query |
|---|---|---|---|---|---|---|
| Adjacency List | O(|V|+|E|) | O(1) | O(1) | O(|V| + |E|) | O(|E|) | O(|V|) |
| Incidence List | O(|V|+|E|) | O(1) | O(1) | O(|E|) | O(|E|) | O(|E|) |
| Adjacency Matrix | O(|V|^2) | O(|V|^2) | O(1) | O(|V|^2) | O(1) | O(1) |
| Incidence Matrix | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|E|) |
Storing information in a way that is quick to retrieve, add, and search on, is a very important technique to master. Here is what you need to know about heap data structures:
Big O Notation Calculator
| Heaps | Heapify | Find Max | Extract Max | Increase Key | Insert | Delete | Merge |
|---|---|---|---|---|---|---|---|
| Sorted Linked List | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Unsorted Linked List | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap | - | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
| Fibonacci Heap | - | O(1) | O(log(n))* | O(1)* | O(1) | O(log(n))* | O(1) |
